ما هو التيار المتردد وكيف يختلف عن التيار المباشر
التيار المتردد ، في المقابل العاصمة الحالية، يتغير باستمرار من حيث الحجم والاتجاه ، وتحدث هذه التغييرات بشكل دوري ، أي أنها تكرر نفسها على فترات متساوية تمامًا.
للحث على مثل هذا التيار في الدائرة ، استخدم مصادر التيار المتناوب التي تخلق EMF متناوبًا ، يتغير بشكل دوري في الحجم والاتجاه ، وتسمى هذه المصادر بالمولدات.
في التين. يوضح الشكل 1 مخطط الجهاز (نموذج) من أبسط المولد.
إطار مستطيل الشكل مصنوع من سلك نحاسي ، ومثبت على المحور ومدار في الميدان باستخدام حزام سير مغناطيس… نهايات الإطار ملحومة بحلقات نحاسية ، والتي تدور مع الإطار تنزلق على ألواح التلامس (الفرش).
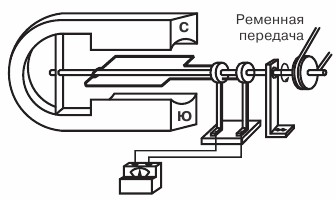
الشكل 1. رسم تخطيطي لأبسط المولد
دعنا نتأكد من أن مثل هذا الجهاز هو بالفعل مصدر EMF المتغير.
افترض أن المغناطيس يخلق بين أقطابها مجال مغناطيسي موحد، أي أن كثافة خطوط المجال المغناطيسي في كل جزء من المجال هي نفسها.بالتناوب ، يتقاطع الإطار مع خطوط قوة المجال المغناطيسي في كل من جانبيها أ و ب المستحثة EMF.
لا يعمل الجانبان c و d من الإطار ، لأنه عندما يدور الإطار ، لا يعبران خطوط قوة المجال المغناطيسي وبالتالي لا يشاركان في إنشاء EMF.
في أي لحظة من الزمن ، تكون المجالات الكهرومغناطيسية التي تحدث في الجانب أ هي عكس اتجاه المجالات الكهرومغناطيسية التي تحدث في الجانب ب ، ولكن في الإطار تعمل كلتا المجالات الكهرومغناطيسية وفقًا لمجموع المجالات الكهرومغناطيسية وتضيفها ، أي الناجم عن الإطار بأكمله.
من السهل التحقق مما إذا كنا نستخدم القاعدة اليمنى التي نعرفها لتحديد اتجاه EMF.
للقيام بذلك ، ضع راحة اليد اليمنى بحيث تواجه القطب الشمالي للمغناطيس ، ويتزامن الإبهام المنحني مع اتجاه حركة ذلك الجانب من الإطار الذي نريد تحديد اتجاه EMF فيه. ثم سيتم الإشارة إلى اتجاه EMF فيه بأصابع اليد الممدودة.
مهما كان موضع الإطار نحدد اتجاه EMF في الجانبين a و b ، فهما دائمًا يضيفان ويشكلان إجمالي EMF في الإطار. في الوقت نفسه ، مع كل دوران للإطار ، يتغير اتجاه إجمالي EMF فيه إلى العكس ، حيث يمر كل جانب من جوانب العمل للإطار في دورة واحدة تحت أقطاب مختلفة من المغناطيس.
يتغير حجم EMF المستحث في الإطار أيضًا مع تغير المعدل الذي تتقاطع فيه جوانب الإطار مع خطوط المجال المغناطيسي. في الواقع ، في اللحظة التي يقترب فيها الإطار من وضعه الرأسي ويمرره ، تكون سرعة عبور خطوط القوة على جانبي الإطار هي الأعلى ، ويتم إحداث أكبر emf في الإطار.في تلك اللحظات ، عندما يمر الإطار في موضعه الأفقي ، يبدو أن جوانبه تنزلق على طول خطوط المجال المغناطيسي دون تقاطعها ، ولا يتم إحداث أي EMF.
لذلك ، مع الدوران المنتظم للإطار ، سيتم إحداث EMF فيه ، متغيرًا بشكل دوري من حيث الحجم والاتجاه.
يمكن قياس EMF الذي يحدث في الإطار بواسطة جهاز واستخدامه لإنشاء تيار في الدائرة الخارجية.
استخدام ظاهرة الحث الكهرومغناطيسي، يمكنك الحصول على EMF بالتناوب وبالتالي التيار المتردد.
التيار المتردد للأغراض الصناعية و للإضاءة يتم إنتاجها بواسطة مولدات قوية تعمل بواسطة التوربينات البخارية أو المائية ومحركات الاحتراق الداخلي.
التمثيل البياني للتيارات AC و DC
تجعل الطريقة الرسومية من الممكن تصور عملية تغيير متغير معين حسب الوقت.
يبدأ رسم المتغيرات التي تتغير بمرور الوقت برسم خطين متعامدين بشكل متبادل يسمى محاور الرسم البياني. ثم ، على المحور الأفقي ، على مقياس معين ، يتم رسم الفواصل الزمنية ، وعلى المحور الرأسي ، أيضًا على مقياس معين ، قيم الكمية المراد رسمها (EMF ، الجهد أو التيار).
في التين. 2 رسم بياني للتيار المباشر والتيار المتردد ... في هذه الحالة نقوم بتأخير القيم الحالية والقيم الحالية لاتجاه واحد ، والتي تسمى عادةً موجبة ، تتأخر عموديًا من نقطة تقاطع المحاور O ، ومن هذه النقطة ، الاتجاه المعاكس ، والذي يسمى عادة بالسالب.
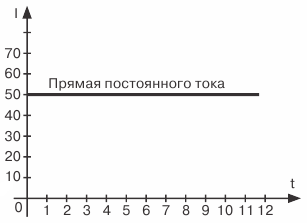
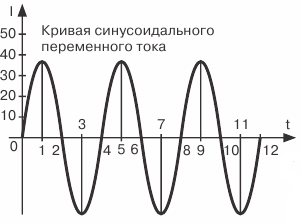الشكل 2. تمثيل رسومي لل DC و AC
تعمل النقطة O نفسها كأصل للقيم الحالية (عموديًا لأسفل ولأعلى) والوقت (أفقيًا يمينًا).بعبارة أخرى ، تتوافق هذه النقطة مع القيمة الصفرية للتيار ونقطة البداية في الوقت التي نعتزم من خلالها تتبع كيف سيتغير التيار في المستقبل.
دعونا نتحقق من صحة ما هو مرسوم في الشكل. 2 و 50 مللي أمبير مؤامرة تيار مستمر.
نظرًا لأن هذا التيار ثابت ، أي أنه لا يغير حجمه واتجاهه بمرور الوقت ، فإن نفس القيم الحالية سوف تتوافق مع لحظات مختلفة من الوقت ، أي 50 مللي أمبير. لذلك ، في اللحظة الزمنية التي تساوي صفرًا ، أي في اللحظة الأولى لملاحظتنا للتيار ، ستكون مساوية لـ 50 مللي أمبير. رسم قطعة تساوي القيمة الحالية 50 مللي أمبير على المحور الرأسي لأعلى ، نحصل على النقطة الأولى من الرسم البياني الخاص بنا.
يجب أن نفعل الشيء نفسه للحظة التالية في الوقت المقابل للنقطة 1 على محور الوقت ، أي التأجيل من هذه النقطة عموديًا إلى أعلى مقطعًا يساوي أيضًا 50 مللي أمبير. ستحدد نهاية المقطع بالنسبة لنا النقطة الثانية من الرسم البياني.
بعد أن قمنا ببناء مماثل لعدة نقاط لاحقة في الوقت المناسب ، نحصل على سلسلة من النقاط ، والتي سيعطي اتصالها خطًا مستقيمًا ، وهو تمثيل رسومي لقيمة تيار ثابتة تبلغ 50 مللي أمبير.
رسم متغير EMF
دعنا ننتقل إلى دراسة الرسم البياني المتغير لـ EMF ... في التين. في الشكل 3 ، يتم عرض إطار يدور في مجال مغناطيسي في الأعلى ، ويرد أدناه تمثيل رسومي للمتغير EMF الناتج.
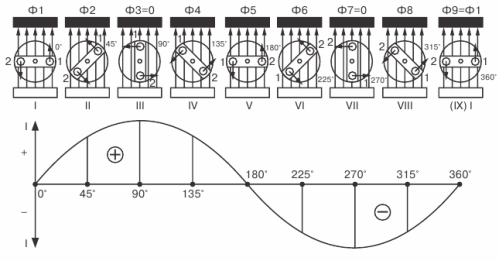الشكل 3. رسم متغير EMF
نبدأ في تدوير الإطار بشكل موحد في اتجاه عقارب الساعة واتباع مسار تغييرات EMF فيه ، مع الأخذ في الاعتبار الوضع الأفقي للإطار كلحظة أولية.
في هذه اللحظة الأولية ، سيكون EMF صفراً لأن جوانب الإطار لا تعبر خطوط المجال المغناطيسي.على الرسم البياني ، يتم تمثيل هذه القيمة الصفرية لـ EMF المقابلة للحظة t = 0 بالنقطة 1.
مع مزيد من التدوير للإطار ، سيبدأ EMF في الظهور فيه وسيزداد حتى يصل الإطار إلى موضعه الرأسي. على الرسم البياني ، سيتم تمثيل هذه الزيادة في EMF من خلال منحنى صعودي سلس يصل إلى ذروته (النقطة 2).
عندما يقترب الإطار من الوضع الأفقي ، فإن EMF فيه سوف ينخفض وينخفض إلى الصفر. على الرسم البياني ، سيتم تصوير هذا على أنه منحنى سلس هبوط.
لذلك ، خلال الوقت المقابل لنصف ثورة للإطار ، كان EMF فيه قادرًا على الزيادة من الصفر إلى القيمة القصوى وتنخفض إلى الصفر مرة أخرى (النقطة 3).
مع مزيد من الدوران للإطار ، ستظهر EMF فيه وتزيد تدريجياً في الحجم ، لكن اتجاهه سيتغير بالفعل إلى العكس ، كما يمكن رؤيته من خلال تطبيق قاعدة اليد اليمنى.
يأخذ الرسم البياني في الاعتبار التغيير في اتجاه EMF ، بحيث يتقاطع المنحنى الذي يمثل EMF مع محور الوقت ويقع الآن أسفل هذا المحور. يزيد EMF مرة أخرى حتى يفترض الإطار وضعًا رأسيًا.
ثم تبدأ EMF في الانخفاض وستصبح قيمتها مساوية للصفر عندما يعود الإطار إلى موضعه الأصلي بعد إكمال دورة كاملة واحدة. على الرسم البياني ، سيتم التعبير عن ذلك من خلال حقيقة أن منحنى EMF ، الذي يصل إلى ذروته في الاتجاه المعاكس (النقطة 4) ، سيلتقي بعد ذلك بمحور الوقت (النقطة 5)
هذا يكمل دورة واحدة من تغيير EMF ، ولكن إذا واصلت تدوير الإطار ، تبدأ الدورة الثانية على الفور ، وتكرر بالضبط الأولى ، والتي بدورها ستتبعها الثالثة ، ثم الرابعة ، وهكذا حتى نتوقف إطار الدوران.
وهكذا ، لكل دوران للإطار ، فإن المجال الكهرومغناطيسي الذي يحدث فيه يكمل دورة كاملة من تغييره.
إذا كان الإطار مغلقًا على بعض الدوائر الخارجية ، فإن تيارًا متناوبًا سيتدفق عبر الدائرة ، وسيبدو الرسم البياني الخاص بها مثل الرسم البياني EMF.
يُطلق على شكل الموجة الناتج موجة جيبية ، ويسمى التيار الكهرومغناطيسي أو الجهد المتغير وفقًا لهذا القانون باسم الجيب الجيبي.
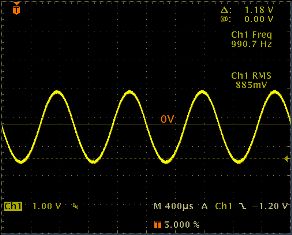
يُطلق على المنحنى نفسه اسم الجيب لأنه تمثيل رسومي لكمية مثلثية متغيرة تسمى الجيب.
تعد الطبيعة الجيبية للتغير الحالي هي الأكثر شيوعًا في الهندسة الكهربائية ، وبالتالي ، عند الحديث عن التيار المتردد ، فهي تعني في معظم الحالات التيار الجيبي.
لمقارنة التيارات المتناوبة المختلفة (المجالات الكهرومغناطيسية والفولتية) ، هناك قيم تميز تيارًا معينًا. هذه تسمى معلمات التيار المتردد.
الفترة والسعة والتردد - معلمات التيار المتردد
يتميز التيار المتردد بمعلمتين - الدورة الشهرية والسعة ، مع معرفة أيهما يمكننا تقدير نوع التيار المتردد وبناء رسم بياني للتيار.
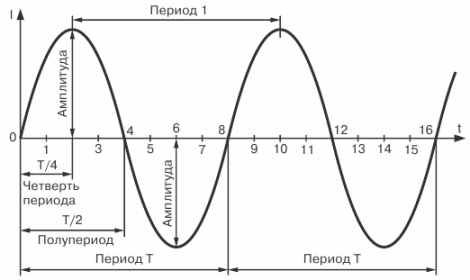
الشكل 4. منحنى التيار الجيبي
الفترة الزمنية التي تحدث خلالها دورة كاملة من التغيير الحالي تسمى الفترة. يتم الإشارة إلى الفترة بالحرف T ويتم قياسها بالثواني.
الفترة الزمنية التي يحدث خلالها نصف دورة كاملة من التغيير الحالي تسمى نصف دورة ، وبالتالي ، فإن فترة تغير التيار (EMF أو الجهد) تتكون من فترتين نصفيتين. من الواضح تمامًا أن جميع فترات نفس التيار المتردد متساوية مع بعضها البعض.
كما يتضح من الرسم البياني ، خلال فترة واحدة من التغيير ، يصل التيار إلى ضعف قيمته القصوى.
تسمى القيمة القصوى للتيار المتردد (EMF أو الجهد) بالسعة أو قيمة الذروة الحالية.
Im و Em و Um هي تسميات شائعة لاتساع التيار و EMF والجهد.
بادئ ذي بدء ، لقد انتبهنا تيار الذروةومع ذلك ، كما يتضح من الرسم البياني ، هناك قيم وسيطة لا حصر لها أصغر من السعة.
تسمى قيمة التيار المتردد (EMF ، الجهد) المقابلة لأي لحظة محددة في الوقت المناسب قيمتها اللحظية.
i و e و u هي تسميات مقبولة بشكل عام للقيم اللحظية للتيار و emf والجهد.
من السهل تحديد القيمة اللحظية للتيار ، وكذلك قيمة الذروة بمساعدة الرسم البياني. للقيام بذلك ، من أي نقطة على المحور الأفقي المقابل للنقطة الزمنية التي نهتم بها ، ارسم خطًا رأسيًا إلى نقطة التقاطع مع المنحنى الحالي ؛ سيحدد الجزء الناتج من الخط العمودي قيمة التيار في وقت معين ، أي قيمته اللحظية.
من الواضح أن القيمة اللحظية للتيار بعد الوقت T / 2 من نقطة بداية الرسم البياني ستكون صفرًا ، وبعد الوقت T / 4 قيمة اتساعها. يصل التيار أيضًا إلى قيمته القصوى ؛ ولكن بالفعل في الاتجاه المعاكس ، بعد وقت يساوي 3/4 طن.
لذا يوضح الرسم البياني كيف يتغير التيار في الدائرة بمرور الوقت وأن قيمة معينة واحدة فقط لكل من حجم واتجاه التيار تتوافق مع كل لحظة من الزمن. في هذه الحالة ، ستكون قيمة التيار عند نقطة زمنية معينة عند نقطة واحدة في الدائرة هي نفسها تمامًا في أي نقطة أخرى في تلك الدائرة.
يطلق عليه عدد الفترات الكاملة التي يحققها التيار في ثانية واحدة من تردد التيار المتردد ويُشار إليه بالحرف اللاتيني f.
لتحديد تواتر التيار المتردد ، أي معرفة عدد فترات تغيير التيار الذي يتم إجراؤه في ثانية واحدة ، من الضروري قسمة ثانية واحدة على وقت فترة واحدة f = 1 / T. معرفة التردد للتيار المتردد ، يمكنك تحديد الفترة الزمنية: T = 1 / f
تردد التيار المتردد يقاس بوحدة تسمى هرتز.
إذا كان لدينا تيار متردد يساوي تردده 1 هرتز ، فإن فترة هذا التيار ستكون ثانية واحدة. على العكس من ذلك ، إذا كانت فترة تغيير التيار هي ثانية واحدة ، فإن تردد مثل هذا التيار هو 1 هرتز.
لذلك قمنا بتعريف معلمات التيار المتردد - الفترة ، والسعة ، والتردد - التي تسمح لك بالتمييز بين التيارات المتناوبة المختلفة ، والمجالات الكهرومغناطيسية ، والجهد ، ورسم الرسوم البيانية الخاصة بهم عند الضرورة.
عند تحديد مقاومة الدوائر المختلفة للتيار المتردد ، استخدم قيمة مساعدة أخرى تميز التيار المتردد ، ما يسمى التردد الزاوي أو الزاوي.
التردد الدائري المرتبط بالتردد f بنسبة 2 pif
دعونا نفسر هذه التبعية. عند رسم مخطط EMF المتغير ، رأينا أن دورانًا كاملًا للإطار ينتج عنه دورة كاملة من تغيير EMF. بعبارة أخرى ، لكي يقوم الإطار بثورة واحدة ، أي أن يدور 360 درجة ، فإنه يستغرق وقتًا يساوي فترة واحدة ، أي T ثانية. ثم ، في ثانية واحدة ، يقوم الإطار بعمل ثورة 360 درجة / T. لذلك ، 360 ° / T هي الزاوية التي يدور من خلالها الإطار في ثانية واحدة ، وتعبر عن سرعة دوران الإطار ، والتي تسمى عادة السرعة الزاوية أو الدائرية.
ولكن نظرًا لأن الفترة T مرتبطة بالتردد f بنسبة f = 1 / T ، فيمكن أيضًا التعبير عن السرعة الدائرية على شكل تردد وستكون مساوية لـ 360 درجة فهرنهايت.
لذلك توصلنا إلى أن 360 درجة فهرنهايت. ومع ذلك ، لتسهيل استخدام التردد الدائري لأي حسابات ، يتم استبدال الزاوية 360 درجة المقابلة لدورة واحدة بتعبير نصف قطري يساوي 2 نقطة في البوصة راديان ، حيث pi = 3.14. لذلك نحصل أخيرًا على 2pif. لذلك ، لتحديد التردد الزاوي للتيار المتردد (EMF أو الجهد) ، يجب ضرب التردد بالهرتز في رقم ثابت 6.28.