التيار المتردد أحادي الطور

الحصول على التيار المتردد

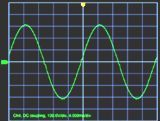إذا تم تدوير السلك A في التدفق المغناطيسي المتكون من قطبي المغناطيس في اتجاه عقارب الساعة (الشكل 1) ، فعندما يعبر السلك خطوط المجال المغناطيسي ، فإنه يستحث e. d. s التي يتم تحديد قيمتها من خلال التعبير

E = Blvsinα ،

حيث B هو الحث المغناطيسي في T ، l هو طول السلك بالمتر ، v هي سرعة السلك بوحدة m / s ، α - الزاوية التي يقطع فيها السلك خطوط المجال المغناطيسي.

دع B و I و v لهذه الحالة تظل ثابتة ، ثم e المستحث. إلخ. ج.يعتمد فقط على الزاوية α التي يعبر فيها السلك المجال المغناطيسي. لذلك ، عند النقطة 1 ، عندما يتحرك السلك على طول خطوط المجال المغناطيسي ، تكون قيمة emf المستحثة. إلخ. سيكون p صفرًا عندما يتحرك السلك إلى النقطة 3 oe. إلخ. v. سيكون ذا أهمية كبيرة ، حيث سيتم عبور خطوط القوة من قبل الموصل في الاتجاه العمودي لهم ، وأخيرًا ، على سبيل المثال ، إلخ. سيصل v. مرة أخرى إلى الصفر إذا تم نقل السلك إلى النقطة 5.

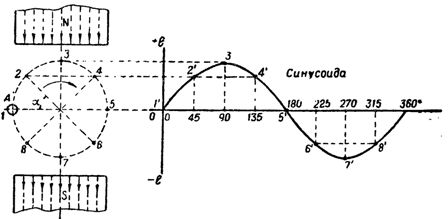
أرز. 1. تغيير المستحثة e. إلخ. ص في ​​سلك يدور في مجال مغناطيسي

عند النقطتين الوسيطة 2 و 4 ، حيث يعبر السلك خطوط القوة بزاوية α = 45 ° ، قيمة emf المستحثة. إلخ. c. سيكون بالمقابل أقل من النقطة 3. وهكذا ، عند لف السلك من النقطة 1 إلى النقطة 5 ، أي بمقدار 180 درجة ، المستحث e. إلخ. v. يتغير من الصفر إلى الحد الأقصى ويعود إلى الصفر.

من الواضح تمامًا أنه عند الدوران الإضافي للسلك A بزاوية 180 درجة (من خلال النقاط 6 و 7 و 8 و 1) ، فإن طبيعة التغيير في e المستحث. إلخ. سيكون p. هو نفسه ، لكن اتجاهه سيتغير إلى الاتجاه المعاكس ، لأن السلك سيعبر خطوط المجال المغناطيسي الموجودة بالفعل أسفل القطب الآخر ، وهو ما يعادل عبورها في الاتجاه الأول المعاكس.

لذلك ، عندما يتم تدوير السلك بزاوية 360 درجة ، يحدث e. إلخ. v. لا يتغير في الحجم طوال الوقت فحسب ، بل يغير اتجاهه مرتين أيضًا.

إذا كان السلك مغلقًا لبعض المقاومة ، فسيظهر السلك كهرباء، متفاوتة أيضًا في الحجم والاتجاه.

التيار الكهربائي ، المتغير باستمرار في الحجم والاتجاه ، يسمى التيار المتردد.

ما هي موجة جيبية؟

طبيعة التغيير ه. إلخ. (تيار) لدورة واحدة من السلك لمزيد من الوضوح ، يتم تمثيلها بيانياً باستخدام منحنى. منذ قيمة البريد. إلخ. ج - بالتناسب مع sinα ، إذن ، بعد تعيين زوايا معينة ، من الممكن ، بمساعدة الجداول ، تحديد قيمة الجيب لكل زاوية ، وعلى المقياس المناسب لإنشاء منحنى لتغيير البريد. إلخ. ج- للقيام بذلك ، على المحور الأفقي سنضع جانباً زوايا دوران السلك ، وعلى المحور الرأسي ، بالمقياس المناسب ، المحرض e. إلخ. مع

إذا تم الإشارة إليه مسبقًا في الشكل.1 قم بتوصيل النقاط بخط منحني ناعم ، ثم سيعطي فكرة عن حجم وطبيعة التغيير في e المستحث. إلخ. (تيار) في أي موضع للموصل في مجال مغناطيسي. يرجع ذلك إلى حقيقة أن قيمة المستحثة e. إلخ. ص.في أي لحظة ، يتم تحديد جيب الزاوية التي يعبر فيها السلك المجال المغناطيسي الموضح في الشكل. منحنى 1 يسمى الجيب ، و e. إلخ. ق - جيبية.

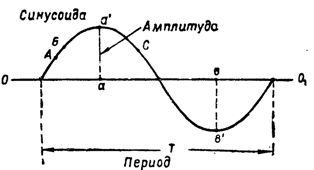
أرز. 2. الجيوب الأنفية وقيمها المميزة

التغييرات التي نظرنا إليها e. إلخ. ج.توافق جيبيًا مع دوران السلك في مجال مغناطيسي بزاوية 360 درجة. عندما يتم تدوير السلك بزاوية 360 درجة التالية ، تحدث التغييرات في e. إلخ. ستظهر s (والتيار) مرة أخرى في موجة جيبية ، أي أنها ستتكرر بشكل دوري.

تبعا لذلك ، بسبب هذا ه. إلخ. ج. يسمى التيار الكهربائي المتردد الجيبي ... من الواضح تمامًا أن الجهد الذي يمكن قياسه بواسطتنا في نهايات السلك A ، في وجود دائرة خارجية مغلقة ، سيتغير أيضًا بطريقة جيبية.

التيار المتردد الذي يتم الحصول عليه عن طريق تدوير سلك في تدفق مغناطيسي أو نظام من الأسلاك المتصلة في ملف يسمى التيار المتردد أحادي الطور.

التيارات المتناوبة الجيبية هي الأكثر استخدامًا في التكنولوجيا. ومع ذلك ، يمكنك العثور على التيارات المتناوبة التي لا تتغير وفقًا لقانون الجيب. تسمى هذه التيارات المتناوبة غير الجيبية.

أنظر أيضا: ما هو التيار المتردد وكيف يختلف عن التيار المباشر

السعة ، الفترة ، تردد التيار المتردد أحادي الطور

القوة الحالية، يتغير على طول الجيب ، يتغير باستمرار. لذا ، إذا كان التيار عند النقطة A (الشكل 2) يساوي 3 أ ، فعند النقطة B سيكون أكبر بالفعل.في نقطة أخرى على الجيب الجيبي ، على سبيل المثال عند النقطة C ، سيكون للتيار الآن قيمة جديدة ، وهكذا.

تسمى قوة التيار في أوقات معينة عندما يتغير على طول الجيوب الأنفية بقيم التيار اللحظي.

يتم استدعاء أكبر قيمة لحظية للتيار المتردد أحادي الطور عندما يتغير على طول السعة الجيبية ... من السهل أن نرى أنه في دورة واحدة من السلك يصل التيار إلى قيمة اتساعه مرتين. إحدى قيم aa "موجبة ويتم رسمها من المحور 001 والأخرى bv" سالبة ويتم سحبها من المحور.

الوقت الذي يتم خلاله المستحث e. إلخ. (أو القوة الحالية) تمر خلال الدورة الكاملة للتغييرات ، ما يسمى بالدورة الشهرية T (الشكل 2). عادة ما يتم قياس الفترة بالثواني.

مقلوب الفترة يسمى التردد (و). بعبارة أخرى، تردد التيار المتردد هو عدد الفترات لكل وحدة زمنية ، أي في ثوان لذلك ، على سبيل المثال ، إذا كان التيار المتردد في غضون ثانية واحدة يفترض نفس القيم والاتجاه عشر مرات ، فإن تردد مثل هذا التيار المتردد سيكون 10 فترات في الثانية.

لقياس التردد ، بدلاً من عدد الفترات في الثانية ، يتم استخدام وحدة تسمى هرتز (هرتز). تردد 1 هرتز يساوي تردد 1 lps / ثانية. عند قياس الترددات العالية ، يكون من الأنسب استخدام وحدة أكبر 1000 مرة من هرتز ، أي. كيلو هرتز (كيلو هرتز) ، أو 1000000 مرة أكبر من هرتز - ميغا هرتز (ميغا هرتز).

يمكن تقسيم التيارات المتناوبة المستخدمة في التكنولوجيا ، اعتمادًا على التردد ، إلى تيارات منخفضة التردد وتيارات عالية التردد.

قيمة جذر متوسط ​​التربيع AC

يسخن التيار المباشر الذي يمر عبر السلك. إذا قمت بتشغيل تيار متناوب عبر السلك ، فسوف يسخن السلك أيضًا.هذا أمر مفهوم ، لأنه على الرغم من أن التيار المتردد يغير اتجاهه طوال الوقت ، فإن إطلاق الحرارة لا يعتمد على الإطلاق على اتجاه التيار في السلك.

عندما يمر التيار المتردد من خلال المصباح الكهربائي ، سوف يتوهج خيوطه. عند التردد القياسي للتيار المتردد البالغ 50 هرتز ، لن يكون هناك وميض للضوء ، لأن خيوط المصباح المتوهج ، ذات القصور الذاتي الحراري ، ليس لديها وقت لتبرد في تلك الأوقات التي يكون فيها التيار في الدائرة صفرًا. أصبح استخدام التيار المتردد بتردد أقل من 50 هرتز للإضاءة الآن غير مرغوب فيه نظرًا لظهور تقلبات غير سارة ومرهقة للعين في شدة المصباح.

استمرارًا لتشبيه التيار المباشر ، يمكننا أن نتوقع أن تيارًا متناوبًا يتدفق عبر سلك يتشكل حوله حقل مغناطيسي. في الواقع ، لا يُنشئ التيار المتردد مجالًا مغناطيسيًا ، ولكن لأن المجال المغناطيسي الذي يخلقه سيكون أيضًا متغيرًا في الاتجاه والحجم.

يتغير التيار المتردد طوال الوقت في كل من الحجم والاتجاه NS. بطبيعة الحال ، فإن السؤال الذي يطرح نفسه هو كيفية قياس المتغير T جيدًا ، وما هي قيمته عند التغيير على طول الجيب الذي يجب اعتباره سببًا لهذا الإجراء أو ذاك.

C لهذا الغرض ، تتم مقارنة التيار المتردد من حيث الإجراء الذي ينتجه مع التيار المباشر ، والذي تظل قيمته دون تغيير أثناء التجربة.

افترض أن تيارًا مباشرًا يتدفق عبر سلك ذو مقاومة ثابتة 10 أ ووجد أن السلك تم تسخينه إلى درجة حرارة 50 درجة.إذا مررنا الآن عبر نفس السلك ليس تيارًا مباشرًا ، بل تيارًا متناوبًا ، وهكذا نختار قيمته (التمثيل ، على سبيل المثال ، مع مقاومة متغيرة) بحيث يتم تسخين السلك أيضًا إلى درجة حرارة 50 درجة ، ثم في في هذه الحالة يمكننا القول أن عمل التيار المتردد يساوي عمل التيار المباشر.

يُظهر تسخين السلك في كلتا الحالتين إلى نفس درجة الحرارة أنه في وحدة زمنية يعطي التيار المتردد في السلك نفس كمية الحرارة مثل التيار المباشر.

تيار جيبي متناوب ينبعث لمقاومة معينة لكل وحدة زمنية نفس كمية الحرارة مثل مكافئ تيار مباشر في الحجم للتيار المباشر ... تسمى هذه القيمة الحالية القيمة الفعالة (Id) أو القيمة الفعالة للتيار المتردد .. لذلك ، على سبيل المثال لدينا ، ستكون القيمة الفعالة للتيار المتردد هي 10 أ ... في هذه الحالة ، ستتجاوز القيم الحالية (الذروة) متوسط ​​القيم في المقدار.

تظهر التجربة والحسابات أن القيم الفعالة للتيار المتردد أصغر من قيم اتساعها في 2 (1.41) مرة. لذلك ، إذا كانت قيمة الذروة للتيار معروفة ، فيمكن تحديد القيمة الفعالة للمعرف الحالي بقسمة سعة Ia الحالية على √2 ، أي Id = Aza / √2

على العكس من ذلك ، إذا كانت قيمة جذر متوسط ​​التربيع للتيار معروفة ، فيمكن حساب قيمة الذروة للتيار ، أي Ia = Azd√2

سوف تنطبق نفس العلاقات على قيم الاتساع وجذر متوسط ​​التربيع لـ e. إلخ. الخامس والجهد: الوحدة = Ea / √2 ، Ud = Uа / √2

غالبًا ما تُظهر أجهزة القياس القيم الفعلية ، لذلك ، عند الترميز ، عادةً ما يتم حذف الفهرس «d» ، لكن يجب ألا تنسى ذلك.

المعاوقة في دوائر التيار المتردد

عندما يكون مستهلكو المحاثة والسعة متصلين بدائرة التيار المتردد ، يجب مراعاة كل من النشطين والمفاعلة (تحدث المفاعلة عندما يكون المكثف قيد التشغيل أو الاختناقات في دائرة التيار المتردد). لذلك ، عند تحديد التيار الذي يمر عبر هذا المستهلك ، من الضروري تقسيم جهد الإمداد بمقاومة الدائرة (المستهلك).

يتم تحديد المعاوقة (Z) لدائرة التيار المتردد أحادية الطور بالصيغة التالية:

Z = √ (R2 + (L - 1 / ωC) 2

حيث R هي المقاومة النشطة للدائرة بالأوم ، L هي محاثة الدائرة في هنري ، C هي سعة الدائرة (مكثف) في الفاراد ، ω - التردد الزاوي للتيار المتردد.

يتم استخدام مستهلكين مختلفين في دوائر التيار المتناوب حيث يكون من الضروري مراعاة القيم الثلاث لـ R أو L أو C أو بعضها فقط. في الوقت نفسه ، يجب مراعاة التردد الزاوي للتيار المتردد.

بالنسبة لبعض المستخدمين ، يمكن فقط أخذ قيم R و L في الاعتبار عند قيم تردد الزاوية المقابلة. على سبيل المثال ، عند تردد تيار متردد يبلغ 50 هرتز ملف الملف اللولبي أو يمكن اعتبار لف المولد فقط على أنه يحتوي على مقاومة نشطة واستقرائية. بمعنى آخر ، السعة في هذه الحالة يمكن إهمالها. ثم يمكن حساب مقاومة التيار المتردد لمثل هذا المستخدم بالصيغة:

Z = √ (R2 + ω2L2)

إذا تم توصيل مثل هذا الملف أو الملف المصمم للتشغيل الحالي المتناوب بتيار مباشر من نفس الجهد ، فسوف يتدفق تيار كبير جدًا عبر الملف ، مما قد يؤدي إلى توليد حرارة كبيرة ، ويمكن أن يتلف عزل الملف على العكس من ذلك ، سوف يتدفق تيار صغير عبر ملف مصمم للعمل في دائرة تيار مباشر ومتصل بدائرة تيار متناوب من نفس الجهد ، ولن يقوم الجهاز الذي يستخدم فيه هذا الملف بتنفيذ الإجراء المطلوب.

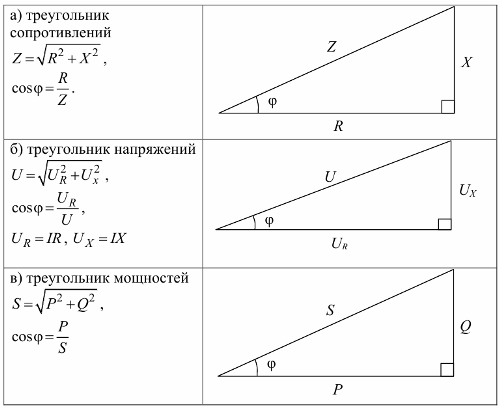
مثلث المقاومة ومثلث الجهد ومثلث القوة: